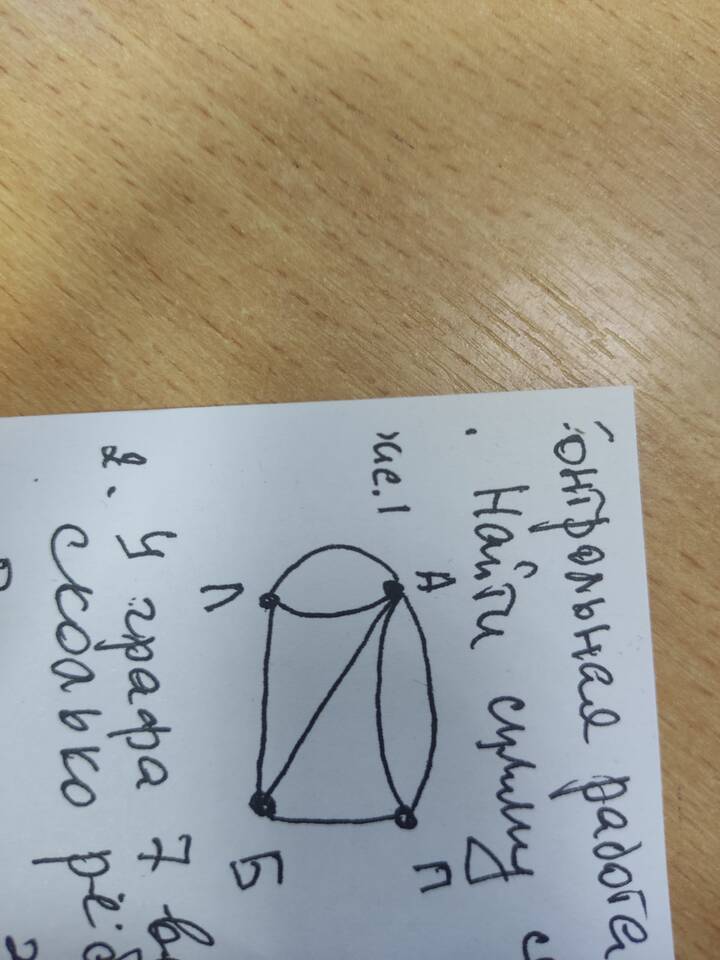
Сумма степеней вершин графа - важная характеристика, используемая в теории графов для анализа свойств и структуры графа. Рассмотрим методы вычисления этой суммы и ее свойства.
Содержание
Основные понятия
- Степень вершины - количество ребер, инцидентных вершине
- Для ориентированных графов различают полустепень исхода и захода
- Петля увеличивает степень вершины на 2
- Изолированная вершина имеет степень 0
Теорема о сумме степеней
Для любого неориентированного графа сумма степеней всех вершин равна удвоенному количеству ребер:
Σdeg(v) = 2E
где deg(v) - степень вершины v, E - количество ребер в графе
Алгоритмы вычисления
По матрице смежности:
- Для каждой вершины vi посчитайте количество единиц в i-й строке
- Сложите полученные значения для всех вершин
- Для графов с петлями добавьте 1 за каждую петлю
По списку ребер:
- Инициализируйте массив степеней нулями
- Для каждого ребра (u,v) увеличьте степени u и v на 1
- Просуммируйте значения в массиве
Пример вычисления
| Граф | Степени вершин | Сумма степеней |
| K3 (полный граф с 3 вершинами) | 2, 2, 2 | 6 = 2×3 |
| Дерево с 4 вершинами | 1, 1, 2, 2 | 6 = 2×3 |
Свойства суммы степеней
- Сумма степеней всегда четна
- Количество вершин нечетной степени четно
- Для регулярных графов (где все степени равны k) сумма равна n×k
- В ориентированном графе сумма полустепеней исхода равна сумме полустепеней захода
Применение в задачах
| Задача | Использование суммы степеней |
| Проверка существования графа | Четность суммы степеней |
| Построение графа | Проверка последовательности степеней |
| Анализ сетей | Определение общей связности |
Вычислительная сложность
- Для матрицы смежности: O(n2)
- Для списка смежности: O(n+m)
- Для списка ребер: O(m)
- где n - число вершин, m - число ребер
Заключение
Сумма степеней вершин графа является фундаментальной характеристикой, позволяющей анализировать свойства графа и проверять его корректность. Знание методов ее вычисления важно для решения широкого круга задач теории графов и анализа сетевых структур.